HASH表与一致性HASH
哈希表的基本认识
哈希表也叫做散列表,是一种数据结构,他提供了快速的查询以及查询操作,无论哈希表中有多少条数据,他的查找的时间复杂度都是O(1)
哈希表是基于数组原理的,所以导致其扩容测成本非常的高,当哈希表被填满的时候,性能下降非常严重
哈希表运用的就是一种转换的思想,将查询的键转换为数组的下标,在哈希表中这个过程通过哈希函数来完成。
举个例子:
我们上学的时候,大家都会有一个学号「1-n号」中的一个号码,如果我们用哈希表来存放班级里面学生信息的话,我们利用学号作为「键」或者「关键字」,这个「键」或者「关键字」就可以直接作为数据的下标,不需要通过哈希函数进行转化。如果我们需要安装学生姓名作为「键」或者「关键字」,这时候我们就需要哈希函数来帮我们转换成数组的下标。
哈希函数
哈希函数的作用就是帮我们把非整型的数据转换为整型来充当数组的下标
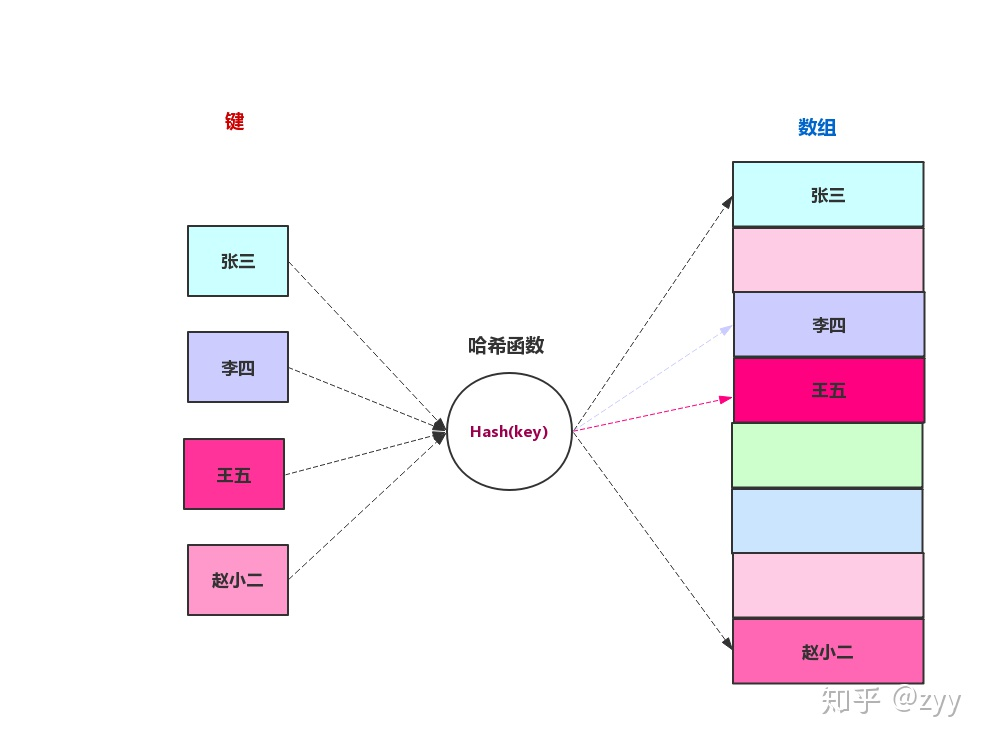
哈希函数要满足如下原则:
- 哈希函数生成的值不能为负数
- 同一个键经过哈希函数运算后得到的下标必须是一致的
通过上面你的描述可以看出,哈希函数生成的下标是可能存在重复的,如student 何student1两个键生成的下标可能相等同为1,那么这时通过哈希表查询的数据就是不准确的,我们把巨大的空间转换为较小的数组空间的时候,不可避免地会出现重复地现象,这个现象就叫做哈希冲突。哈希冲突是不可避免地,我们通过开放地址法与链表法来解决这个问题。
哈希冲突的解决
开放地址法
线性探测
线性探测的插入
一个键经过哈希运算后,准备将其对应的数据插入到计算出来的下标对应的数组的位置时,发现该位置已经有值了,此时会按照顺序依次向下探测下一个下标,直到找到一个空的位置为止
线性探测的查找
通过散列函数计算处键值对应的数组下标,到哈希表中去查找,然后比较对应位置的键值与计算得出的键值,如果相等则匹配到了数据,如果不相等,则依次向下查找,直到找到位置
线性探测的删除
如果直接删除对应下标处的数据的话,会导致后续的查询操作过程中不能查找到正确的值,比如键值a计算得到的哈希值为3,但再插入的时候,3对应的位置已经有值了,依次遍历到位置5后成功插入。那么再删除了3对应位置的值之后,再查询a对应数据的过程中,首先计算出来的下标为3,那么就去3对应的位置找,结果发现时空白,于是认为,键值a,不在该哈希表中,这很显然时不正确的。为了解决这一问题,我们可以为被删除的位置插入一个特殊的标志位,即将该位置的数组下标设为-1来标识该处数据被删除。这样会带来一个问题,如果在线性探测哈希表中做了多次操作,会导致哈希表中充满了学号为-1的数据项,使的哈希表的效率下降,所以很多哈希表中没有提供删除操作,即使提供了删除操作的,也尽量少使用删除函数。

二次探测
在线性探测哈希表中,数据会发生聚集,一旦聚集形成,它就会变的越来越大,那些哈希函数后落在聚集范围内的数据项,都需要一步一步往后移动,并且插入到聚集的后面,因此聚集变的越大,聚集增长的越快。这个就像我们在逛超市一样,当某个地方人很多时,人只会越来越多,大家都只是想知道这里在干什么。
二次探测是防止聚集产生的一种尝试,思想是探测相隔较远的单元,而不是和原始位置相邻的单元。在线性探测中,如果哈希函数得到的原始下标是x,线性探测就是x+1,x+2,x+3……,以此类推,而在二次探测中,探测过程是x+1,x+4,x+9,x+16,x+25……,以此类推,到原始距离的步数平方,为了方便理解,我们来看下面这张图

二次探测消除了线性探测的聚集问题,这种聚集问题叫做原始聚集,然而,二次探测也产生了新的聚集问题,之所以会产生新的聚集问题,是因为所有映射到同一位置的关键字在寻找空位时,探测的位置都是一样的。
比如讲1、11、21、31、41依次插入到哈希表中,它们映射的位置都是1,那么11需要以一为步长探测,21需要以四为步长探测,31需要为九为步长探测,41需要以十六为步长探测,只要有一项映射到1的位置,就需要更长的步长来探测,这个现象叫做二次聚集。
双哈希
双哈希是为了消除原始聚集和二次聚集问题,不管是线性探测还是二次探测,每次的探测步长都是固定的。双哈希是除了第一个哈希函数外再增加一个哈希函数用来根据关键字生成探测步长,这样即使第一个哈希函数映射到了数组的同一下标,但是探测步长不一样,这样就能够解决聚集的问题。

第二个哈希函数必须满足:
- 和第一个哈希函数不一样
- 不能为0
哈希表的容量必须是一个质数:
假设我们哈希表的容量为15,某个**「关键字」**经过双哈希函数后得到的数组下标为0,步长为5。那么这个探测过程是0,5,10,0,5,10,一直只会尝试这三个位置,永远找不到空白位置来存放,最终会导致崩溃。
如果我们哈希表的大小为13,某个**「关键字」**经过双哈希函数后得到的数组下标为0,步长为5。那么这个探测过程是0,5,10,2,7,12,4,9,1,6,11,3。会查找到哈希表中的每一个位置。
使用开放地址法,不管使用那种策略都会有各种问题,开放地址法不怎么使用,在开放地址法中使用较多的是双哈希策略。
链表法
开放地址法中,通过在哈希表中再寻找一个空位解决冲突的问题,还有一种更加常用的办法是使用「链表法」来解决哈希冲突。「链表法」相对简单很多,「链表法」是每个数组对应一条链表。当某项关键字通过哈希后落到哈希表中的某个位置,把该条数据添加到链表中,其他同样映射到这个位置的数据项也只需要添加到链表中,并不需要在原始数组中寻找空位来存储。下图是「链表法」的示意图。

一致性哈希
在进行负载均衡调度的时候,往往用到哈希算法,通过哈希函数,将数据映射到对应的服务器集群上面,传统的哈希函数存在着可扩展性差,容错能力差的问题
可扩展性
假设有 3 个服务器节点编号 [0 - 2],6 个缓存键值对编号 [1 - 6],则完成哈希映射之后,三个缓存数据映射情况如下:
哈希计算公式:key % 节点总数 = Hash节点下标
1 % 3 = 1
2 % 3 = 2
3 % 3 = 0
4 % 3 = 1
5 % 3 = 2
6 % 3 = 0

每个连接都均匀的分散到了三个不同的服务器节点上,看起来很完美!
但是,在分布式集群系统的负载均衡实现上,这种模型有两个问题:
扩展能力差
为了动态调节服务能力,服务节点经常需要扩容缩容。打个比方,如果是电商服务,双十一期间的服务机器数量肯定要比平常大很多,新加进来的机器会使原来计算的哈希值不准确,为了达到负载均衡的效果,要重新计算并更新哈希值,对于更新后哈希值不一致的缓存数据,要迁移到更新后的节点上去。
假设新增了 1 个服务器节点,由原来的 3 个服务节点变成 4 个节点编号 [0 - 3],哈希映射情况如下:
哈希计算公式:key % 节点总数 = Hash节点下标
1 % 4 = 1
2 % 4 = 2
3 % 4 = 3
4 % 4 = 0
5 % 4 = 1
6 % 4 = 2
可以看到后面三个缓存 key :4、5、6 对应的存储节点全部失效了,这就需要把这几个节点的缓存数据迁移到更新后的节点上 (费时费力) ,也就是由原来的节点 [1, 2, 0] 迁移到节点 [0, 1, 2],迁移后存储示意图如下:

容错能力不佳
线上环境服务节点虽然有各种高可用性保证,但还是是有宕机的可能,即使没有宕机也有缩容的需求。不管是宕机和缩容都可以归结为服务节点删除的情况,下面分析下服务节点删除对负载均衡哈希值的影响。
假设删除 1 个服务器节点,由最初的 3 个服务节点变成 2 个,节点编号 [0 - 1],哈希映射情况如下:
哈希计算公式:key % 节点总数 = Hash节点下标
1 % 2 = 1
2 % 2 = 0
3 % 2 = 1
4 % 2 = 0
5 % 2 = 1
6 % 2 = 0
下图展示普通哈希负载均衡算法在一个节点宕机时候,导致的的缓存数据迁移分布

如图所见,在这个例子中,仅仅删除了一个服务节点,也导致了哈希值的大面积更新,哈希值的更新也是意味着节点缓存数据的迁移。
一致性哈希
一句话概括一致性哈希:就是普通取模哈希算法的改良版,哈希函数计算方法不变,只不过是通过构建环状的 Hash 空间代替普通的线性 Hash 空间。具体做法如下:
首先,选择一个足够大的Hash空间(一般是 0 ~ 2^32)构成一个哈希环。

然后,对于缓存集群内的每个存储服务器节点计算 Hash 值,可以用服务器的 IP 或 主机名计算得到哈希值,计算得到的哈希值就是服务节点在 Hash 环上的位置。

最后,对每个需要存储的数据 key 同样也计算一次哈希值,计算之后的哈希也映射到环上,数据存储的位置是沿顺时针的方向找到的环上的第一个节点。下图举例展示了节点存储的数据情况,我们下面的说明也是基于目前的存储情况来展开。

原理讲完了,来看看为什么这样的设计能解决上面普通哈希的两个问题。
扩展能力提升
前面我们分析过,普通哈希算法当需要扩容增加服务节点的时候,会导致原油哈希映射大面积失效。现在,我们来看下一致性哈希是如何解决这个问题的。
如下图所示,当缓存服务集群要新增一个节点node3时,受影响的只有 key3 对应的数据 value3,此时只需把 value3 由原来的节点 node0 迁移到新增节点 node3 即可,其余节点存储的数据保持不动。

容错能力提升
普通哈希算法当某一服务节点宕机下线,也会导致原来哈希映射的大面积失效,失效的映射触发数据迁移影响缓存服务性能,容错能力不足。一起来看下一致性哈希是如何提升容错能力的。
如下图所示,假设 node2 节点宕机下线,则原来存储于 node2 的数据 value2 和 value5 ,只需按顺时针方向选择新的存储节点 node0 存放即可,不会对其他节点数据产生影响。一致性哈希能把节点宕机造成的影响控制在顺时针相邻节点之间,避免对整个集群造

一致性哈希优化
存在的问题
上面展示了一致性哈希如何解决普通哈希的扩展和容错问题,原理比较简单,在理想情况下可以良好运行,但在实际使用中还有一些实际问题需要考虑,下面具体分析。
数据倾斜
试想一下若缓存集群内的服务节点比较少,就像我们例子中的三个节点,而哈希环的空间又有很大(一般是 0 ~ 2^32),这会导致什么问题呢?
可能的一种情况是,较少的服务节点哈希值聚集在一起,比如下图所示这种情况 node0 、node1、node2 聚集在一起,缓存数据的 key 哈希都映射到 node2 的顺时针方向,数据按顺时针寻找存储节点就导致全都存储到 node0 上去,给单个节点很大的压力!这种情况称为数据倾斜。

节点雪崩
数据倾斜和节点宕机都可能会导致缓存雪崩。
拿前面数据倾斜的示例来说,数据倾斜导致所有缓存数据都打到 node0 上面,有可能会导致 node0 不堪重负被压垮了,node0 宕机,数据又都打到 node1 上面把 node1 也打垮了,node1 也被打趴传递给 node2,这时候故障就像像雪崩时滚雪球一样越滚越大。
还有一种情况是节点由于各种原因宕机下线。比如下图所示的节点 node2 下线导致原本在node2 的数据压到 node0 , 在数据量特别大的情况下也可能导致节点雪崩,具体过程就像刚才的分析一样。
总之,连锁反应导致的整个缓存集群不可用,就称为节点雪崩。

虚拟节点
那该如何解决上述两个棘手的问题呢?可以通过「虚拟节点」的方式解决。
所谓虚拟节点,就是对原来单一的物理节点在哈希环上虚拟出几个它的分身节点,这些分身节点称为「虚拟节点」。打到分身节点上的数据实际上也是映射到分身对应的物理节点上,这样一个物理节点可以通过虚拟节点的方式均匀分散在哈希环的各个部分,解决了数据倾斜问题。
由于虚拟节点分散在哈希环各个部分,当某个节点宕机下线,他所存储的数据会被均匀分配给其他各个节点,避免对单一节点突发压力导致的节点雪崩问题。
下图展示了虚拟节点的哈希环分布,其中左边是没做虚拟节点情况下的节点分布,右边背景色绿色两个的 node0 节点是 node0 节点的虚拟节点;背景色红色的 node1 节点是 node1 的虚拟节点。


